2023. 3. 27. 19:02ㆍ자료구조 및 알고리즘/바킹독 정리
BFS 강의
두 자료 구조를 묶어서 가지고 다닐 수 있는 pair STL
#include <iostream>
using namespace std;
int main(void) {
pair<int, int> t1 = make_pair(10, 13);
pair<int, int> t2 = {4, 6}; // C++11
cout << t2.first << ' ' << t2.second << '\n';
if(t2 < t1) cout << "t2 < t1"; // t2<t1BFS에서는 큐를 쓰는데 큐에 좌표를 넣을 때 pair를 사용
BFS는 모든 노드를 방문하기 위한 거...
BFS 코드는 다음과 같다.
#include <iostream>
#include <queue>
using namespace std;
#define X first
#define Y second
int board[502][502]={{1,1,1,0,1,0,0,0,0,0},
{1,0,0,0,1,0,0,0,0,0},
{1,1,1,0,1,0,0,0,0,0},
{1,1,0,0,1,0,0,0,0,0},
{0,1,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0} }; // 1이 파란 칸, 0이 빨간 칸에 대응
bool vis[502][502]; // 해당 칸을 방문했는지 여부를 저장
int n=7, m=10; // n=행의 수, m=열의 수
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1}; // 상하좌우 네 방향을 의미
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
queue<pair<int, int>> Q;
vis[0][0]=1; // (0,0)을 방문했다고 명시
Q.push({0,0}); // 큐에 시작점인 (0,0)을 삽입
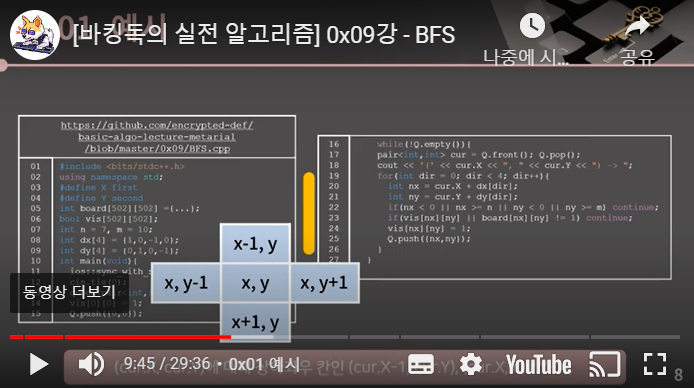
while(!Q.empty()){
pair<int, int> cur =Q.front(); Q.pop(); // 프론트 확인하고 빼라
cout<<'('<<cur.X<<", "<<cur.Y<<") -> ";
for(int dir=0; dir<4; dir++){ // 상하좌우 칸 살펴본다.
int nx = cur.X+dx[dir];
int ny=cur.Y+dy[dir]; // nx, ny에 dir에서 정한 방향의 인접한 칸의 좌표가 들어감
if(nx<0 || nx>=n || ny<0 || ny>=m) continue; // 범위 밖일 경우 넘어감
if(vis[nx][ny]||board[nx][ny]!=1) continue; // 이미 방문한 칸이거나 파란 칸이 아닐 경우
vis[nx][ny]=1; // (nx, ny)를 방문했다고 명시
Q.push({nx, ny});
}
}
}
[BOJ 1926]
https://www.acmicpc.net/problem/1926
1926번: 그림
어떤 큰 도화지에 그림이 그려져 있을 때, 그 그림의 개수와, 그 그림 중 넓이가 가장 넓은 것의 넓이를 출력하여라. 단, 그림이라는 것은 1로 연결된 것을 한 그림이라고 정의하자. 가로나 세로
www.acmicpc.net
1. 상하좌우로 연결된 그림의 크기를 알아내기
큐에서 pop을 몇 번 하는지 세면 1번을 구할 수 있다. - 그렇네
while(!Q.empty()){
pair<int, int> cur =Q.front(); Q.pop(); mx++;// 프론트 확인하고 빼라
// pop의 횟수가 그림의 크기다.2. 도화지에 있는 모든 그림을 찾아내기
내가 더 몰랐던 부분
이중 포문을 돌리면서 BFS의 시작점이 될 수 있는 곳을 찾는다.
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(board[i][j]==0 || vis[i][j]) continue; // 방문했거나 빨간 칸이면 시작점이 될 수 없다.
num++; // 그림의 개수 늘려주기
queue<pair<int int>> Q;
vis[i][j]=1; // (i,j)을 방문했다고 명시
Q.push({i,j}); // 큐에 시작점인 (i,j)을 삽입
int area=0;
while(!Q.empty()) {
중략...
중략한 내용은 큐를 pop하고 push 하는 내용
각 파란칸 딱 한번만 들어가서 시간 복잡도는 O(nm)
코드는
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
#define X first
#define Y second
int board[502][502]; // 1이 파란 칸, 0이 빨간 칸에 대응
bool vis[502][502]; // 해당 칸을 방문했는지 여부를 저장
int n, m; // n=행의 수, m=열의 수
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1}; // 상하좌우 네 방향을 의미
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>n>>m; // 입출력 받기
// 배열 입출력 트릭
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin>> board[i][j];
int mx=0; // 그림 넓이 최대
int num=0; // 그림의 개수
// 이중 포문으로 시작점이 될 수 있는지 보자.
for(int i=0; i<n;i++){
for(int j=0; j<m; j++){
if(board[i][j]==0 || vis[i][j]) continue; // 방문했거나 빨간칸이면 시작점이 될 수 없다.
num++;
queue<pair<int, int>> Q;
vis[i][j]=1; // (i,j)을 방문했다고 명시
Q.push({i,j}); // 큐에 시작점인 (i,j)을 삽입
int area=0;
while(!Q.empty()){
area++;
pair<int, int> cur =Q.front(); Q.pop(); // 프론트 확인하고 빼라
// pop의 횟수가 그림의 크기다.
for(int dir=0; dir<4; dir++){ // 상하좌우 칸 살펴본다.
int nx = cur.X+dx[dir];
int ny=cur.Y+dy[dir]; // nx, ny에 dir에서 정한 방향의 인접한 칸의 좌표가 들어감
if(nx<0 || nx>=n || ny<0 || ny>=m) continue; // 범위 밖일 경우 넘어감
if(vis[nx][ny]||board[nx][ny]!=1) continue; // 이미 방문한 칸이거나 파란 칸이 아닐 경우
vis[nx][ny]=1; // (nx, ny)를 방문했다고 명시
Q.push({nx, ny});
}
}
mx=max(mx, area);
}
}
cout<<num<<'\n'<<mx;
}
다음으로 BOJ 2178
https://www.acmicpc.net/problem/2178
2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net
다차원 배열에서 거리 측정
이해하고 다시 이해했는지 복기 해보기
붙여서 받으니 string으로 받는다.
string board[102]; // 숫자가 붙여서 입력되므로 string 배열로 해준다.
원점으로부터 거리의 배열 dist는 전체 -1로 초기화해준다. ) fill 함수 이용 - 0x03강 참고
시작점은 (0,0)이므로 dist[0][0]=0;으로 초기화해주고 큐에 (0,0)을 pair로 넣어준다.
for(int i=0; i<n; i++) fill(dist[i], dist[i]+m, -1);
queue<pair<int, int>> Q;
Q.push({0,0});
dist[0][0]=0;큐에 시작점이 푸시가 되고 BFS를 도는 코드
상하좌우 nx, ny가 체크 되면 dist를 +1해준다.
while(!Q.empty()){
auto cur=Q.front(); Q.pop();
for(int dir=0; dir<4; dir++){
int nx = cur.X+dx[dir];
int ny = cur.Y+dy[dir];
if(nx<0 || nx>=n || ny<0|| ny>=m) continue;
if(dist[nx][ny]>=0 || board[nx][ny]!='1') continue;
dist[nx][ny]=dist[cur.X][cur.Y]+1;
Q.push({nx,ny});
}
}
dist는 원점으로부터 거리를 나타내서 (0,0)에서는 0이므로 dist[n-1][m-1]+1을 출력해야 된다.
cout<<dist[n-1][m-1]+1; // 문제의 특성상 거리+1이 정답
전체코드는
#include <iostream>
#include <queue>
using namespace std;
#define X first
#define Y second
string board[102]; // 숫자가 붙여서 입력되므로 string 배열로 해준다.
int dist[102][102];
int n,m;
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1};
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>n>>m;
for(int i=0; i<n; i++)
cin>>board[i];
for(int i=0; i<n; i++) fill(dist[i], dist[i]+m, -1);
queue<pair<int, int>> Q;
Q.push({0,0});
dist[0][0]=0;
while(!Q.empty()){
auto cur=Q.front(); Q.pop();
for(int dir=0; dir<4; dir++){
int nx = cur.X+dx[dir];
int ny = cur.Y+dy[dir];
if(nx<0 || nx>=n || ny<0|| ny>=m) continue;
if(dist[nx][ny]>=0 || board[nx][ny]!='1') continue;
dist[nx][ny]=dist[cur.X][cur.Y]+1;
Q.push({nx,ny});
}
}
cout<<dist[n-1][m-1]+1; // 문제의 특성상 거리+1이 정답
}
7576번 토마토 문제 - 시작점이 여러 개인 문제 유형
https://www.acmicpc.net/problem/7576
바킹독 선생님 - 토마토가 익어가는 상황 자체가 BFS를 하는 것과 똑같기도 하고, 토마토가 다 익기까지 필요한 최소 일수를 구하려면 모든 익지 않은 토마토들에 대해 가장 가깝게 위치한 익은 토마토까지의 거리를 구해야한다는 관점에서 살펴봐도 마찬가지로 BFS를 활용할 수 있겠다는 생각이 들 것입니다.
그래서 만약 익은 토마토가 1개였다면 앞의 미로 탐색 문제랑 비슷하게 익은 토마토가 있는 곳을 시작점으로 해서 BFS를 돌려 쉽게 해결이 가능할텐데 이 문제에서는 익은 토마토의 갯수가 여러 개일 수 있습니다. 각 익은 토마토들에 대해 해당 위치를 시작점으로 하는 BFS를 한 번씩 다 돌리는 방법을 떠올릴 수 있지만, 그러면 BFS의 시간복잡도가 O(NM)이고 익은 토마토 또한 최대 NM개가 있을 수 있으니 총 O(N2M2)이 되어 시간 내로 해결이 안될 것입니다. 과연 어떻게 문제를 해결할 수 있을까요?
지금까지의 상황을 다시 정리해보면 우리는 지금 시작점이 여러 개인 BFS를 돌 수 있어야합니다. 그리고 해결법은 의외로 간단한데, 그냥 모든 시작점을 큐에 넣고 앞에서 한 것과 똑같이 BFS를 돌면 끝입니다. 지금 슬라이드에서의 그림을 보면 파란색은 익지 않은 토마토, 초록색은 익은 토마토, 빨간색은 빈 칸을 의미합니다. 현재 익은 토마토가 2개가 있는데, 그 2개를 큐에 넣어두고 BFS를 돌리면 이렇게 자연스럽게 거리가 잘 구해지게 됩니다.
익은 토마토 값은 넣고 익지 않은 거는 -1로 둔다.
익은 토마토가 미로 문제, 그림 문제에서의 시작점이 되어서 Queue에 push 하고
익지 않은 거는 fill을 이용해 -1로 채운다.
if(board[i][j] == 1)
Q.push({i,j});
if(board[i][j] == 0)
dist[i][j] = -1;시작점이 여러 개면, 여러 개의 시작점을 Queue에다가 push한다!!
불 문제
3/23 다른 문제보다 어려워서 이해가 더 필요
출처) https://blog.encrypted.gg/941
[실전 알고리즘] 0x09강 - BFS
안녕하세요 여러분, 드디어 올 것이 왔습니다. 마음의 준비를 단단히 하셔야 합니다.. 드디어 실전 알고리즘 강의에서 첫 번째 고비에 도달했는데 이 강의와 함께 이번 고비를 잘 헤쳐나가면 좋
blog.encrypted.gg
다른 거 더 참고할 것) https://gdlovehush.tistory.com/427
0x09강 - BFS
목차 0x00 BFS 알고리즘 설명 0x01 예시 0x02 응용1 - 거리 측정 0x03 응용2 - 시작점이 여러 개일 때 0x04 응용3 - 시작점이 두 종류일 때 0x05 응용4 - 1차원에서의 BFS 0x00 BFS 알고리즘 Breadth-First Search 너비
gdlovehush.tistory.com
'자료구조 및 알고리즘 > 바킹독 정리' 카테고리의 다른 글
| [바킹독 시뮬레이션] 정리 중 아직은 뉴비 (0) | 2023.04.08 |
|---|---|
| [바킹독 BFS] BFS 기본 문제 유형 분석 (0) | 2023.04.03 |
| [바킹독] Deque 정리 (0) | 2023.03.03 |
| 큐 강의 정리 (0) | 2023.02.24 |
| [바킹독 강의]스택 정리 (1) | 2023.02.15 |